| Our group is a part of a multidisciplinary team that is developing a new mesoscale-level massively-parallel computational method (Ferret) for simulating the properties of materials possessing coupled elastic, polar and magnetic degrees of freedom and subject to a wide variety of applied elastic, electric and thermal boundary conditions [1]. The question of how the spatial inhomogeneities present in these materials on the length scale of hundreds of nanometers to hundreds of micrometers influence their behavior is of paramount importance for the future technological applications. Although these systems are being actively investigated experimentally, the capability to predictively evaluate and optimize their useful properties is sorely lacking, because computationally-intensive quantum mechanical simulation techniques cannot operate on the length and time scales needed to study the complex behavior of such patterned heterostructures. Instead, their properties can be investigated by far less computationally expensive mesoscopic methods that provide a coarse-grained description of materials in the intermediate region between the sizes of atoms/molecules and bulk structures measuring micrometers. However, even on this descriptive level, solving the equations for complex shapes with elasticity, heat, and electro/magnetostatics all coupled together presents a formidable set of computational challenges.The core of our software toolchain is the Multiphysics Object-Oriented Software Environment (MOOSE) [2] developed at Idaho National Laboratory. MOOSE allows a rapid development of coupled physics models that can be interfaced with mesh generation and visualization software, and has a proven record of efficient scaling of execution of phase-field simulation codes to 10K nodes [3, 4]. MOOSE incorporates a library of finite-element basis functions and a host of standard computational kernels discretizing many of the common equations of mathematical physics. Furthermore, it is extensible via addition of new kernels, which allows us to augment MOOSE with custom numerical discretizations and physical models, including modules for the studies of non-linear elasticity, porosity and evolving crystalline grain shapes.Below, we show a number of images from our work that include development of structural models for heterogeneous materials and nanostuctures, and numerical modeling of their static and time-dependent properties. |
Models of grainy matter produced by Voronoi tesselation |
 |
| A variety of structural models of grainy matter are utilized in our mesoscale simulations. All the models shown here are created by the process of Voronoi tesselation of the appropriate geometrical shapes, as implemented in voro++ package, and visualized and meshed in Cubit. Top row: a very simple model with a few quasi-2D grains in a brick, displayed with grains only, or with an overlayed crude tetrahedron mesh. Middle row: a thin film with quasi-2D grains, shown either with or without the overlayed tetrahedron mesh. Bottom row, left: a brick with 3D grains meshed with tetrahedrons; right: a quasi-2D grain partitioning done on a spherical shell. One of the grains was removed to provide a better view of an empty core. |
Energy harvesting with PFM cantilevers (in collaboration with Seungbum Hong, ANL) |
In this project, only the elastic properties of cantilevers (with no coupling to polar degrees of freedom, if any are available) are explored. We can also estimate the frequencies and distortion patterns of the low-energy cantilever vibrational modes under a variety of applied boundary conditions.
Related publications:
|
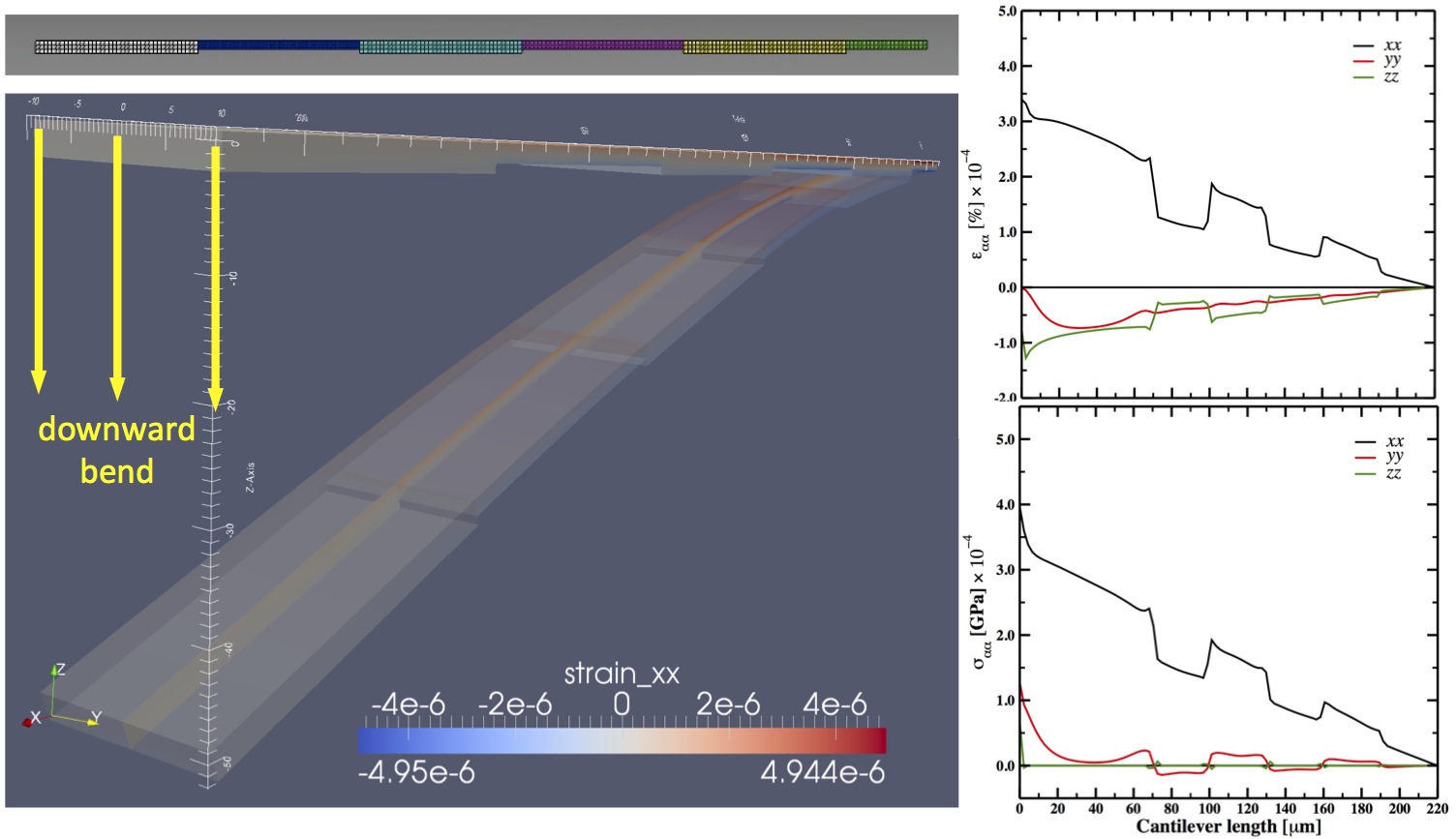 |
| Left: Elastic strain field map (the xx tensor component) in a haircomb-shaped silicon cantilever (approx. 220 × 20 × 3μm) that is clamped at one end and bent down on the other. Both crystallographic anisotropy and inhomogeneous damage of the elastic properties of the silicon sample due to focused ion beam machining are taken into account. Vibrational frequency of the bending mode was computed to be 52 kHz. Right: Changes in elastic strain (top) and stress (bottom) profiles along the cantilever length. Curves for all the diagonal tensor components are shown. |
Here are links to some cantilever vibration animations made by Shiyuan Gu:
|
Mesoscale modeling of functional properties of core-shell nanoparticles |
| We studied variation of stress and strain fields in two popular core-shell nanoparticle (CSNP) materials combinations, Zn-ZnO and ZnO-TiO2, using MOOSE finite-element framework. Taking into account the contribution of surface free energy and the elastic mismatch of the core and shell, we observe an imprinting effect within the shell structure that produces a wide variation of strains. The latter in turn leads to broadening of the sharp direct band gap edges of the bulk semiconductor. We show that a variety of factors, such as particle size, core-to-shell volume ratio, applied hydrostatic pressure, shell microstructure, as well as the effect of elastic anisotropy, can influence the distribution of optical band gap values throughout the particle.
Related publications:
|
 ![ZnOstress_[000]](https://satori-ims.media.uconn.edu/wp-content/uploads/sites/269/2013/12/ZnOstress_000-300x179.png) 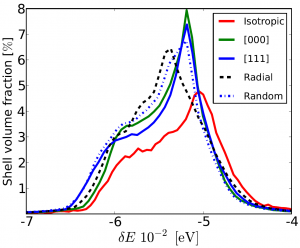 |
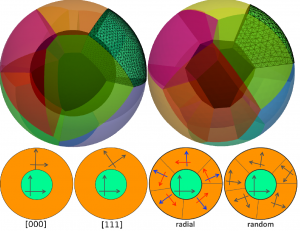
| Left: Sketches of polycrystalline-core CSNP models with spherical and faceted monocrystalline cores. Center: A three-dimensional map of the principal stress field σzz within a ZnO-TiO2 CSNP with a spherical core. Right: A histogram plot showing distribution of band-gap energies throughout the shell region of a Zn-ZnO CSNP for a variety of different shell morphologies at vanishing external pressure. |
Ferroelectric materials and nanostructures: mesoscale simulations with Landau-Ginzburg thermodynamic potentials |
| To get things started, we have recently used a semianalytic approach combined with microscopic Landau-Ginzburg-Devonshire free energy functional theory to demonstrate that the domain structure in nano-scale disks made of the recently predicted layered perovskite PbSr2Ti2O7 [see S. M. Nakhmanson and I. Naumov, Phys. Rev. Lett. 104, 097601 (2010)] can be varied between uniform polarization and a vortex structure, analogous to vortices in soft magnetic disks.
Related publications:
|
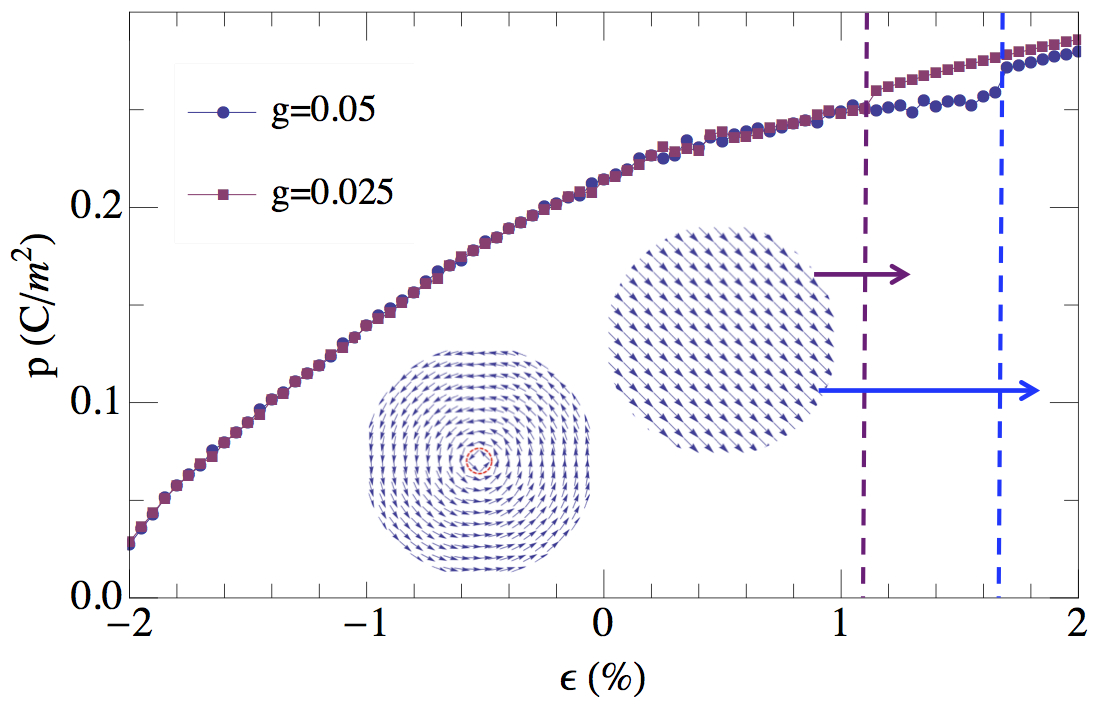 |
| The magnitude of ferroelectric polarization density p in PbSr2Ti2O7 disks with aspect ratio g = L/R = 0.05 and 0.025 as a function of biaxial planar strain ε (%) at T = 0 K. Here the disk thickness L is set to 10 nm. The transition from vortex (actually, doughnut, since the topology of this state is not the same as that of a proper vortex; see publication for more details) to uniform polarization is denoted by the vertical dashed lines, occurring at ε ≈ 1.7% and 1.1% for g = 0.05 and 0.025 disks, respectively. |
References:
|